本文重点讲解一下思路中比较容易卡顿的位置。状态转移方程这篇题解有着详细的讲解,从推导到优化,这里就不赘述了。
反向建边
我们反向建立边,也就是建立 的边,表示 限制 ,这样的好处是一棵外向树,每个节点有一个入度和多个出度,符合正常人的习惯。
这还带来一个好处,就是链式前向星不需要开二倍空间了,而在删去边的部分也不用考虑双向边带来的麻烦。
式返祖找环
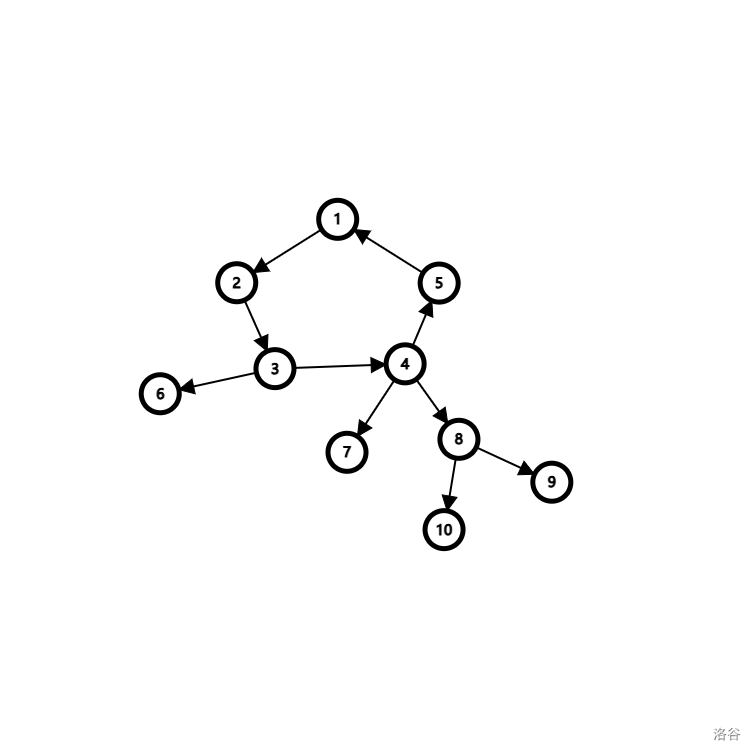
如下图所示,例如我们从 号节点开始向上跳,则路径是:
注意建边是反向建边,返祖就是逆流而上: 。我们在返祖的过程中用 数组标记走过的点,则遇到一个标记过的点就是环上的一端,而此时的位置就是另一端。还是很显然的,因为不会经过自己的儿子,所以这一定是一条逆向的返祖边。
这个方法非常高效,不需要遍历整棵树,而且只需要知道 信息就可以了。不过一般不会直接告诉 信息,导致适用范围并不是非常广泛。

基环树处理方式的选择
我们对于基环树的处理无非两种:
- 删去一条边,当作树进行处理,然后特殊统计删去的边对结果的影响;
- 分成环上问题以及树上问题(环上节点的子树)。
这个地方显然用第二种是不方便的,这样状态转移方程考虑的非常多。包括子树根节点的选或不选,环上节点的选或不选,以及多种多样的依赖关系。
使用第一种方法就很简单了,因为有“强制”策略的存在。
动态规划的强制策略
我们在城市环路中认识了通过赋值为 做到在状态转移中强制不选取,而这个地方是另一种方法:两次树形动态规划。分别统计依赖非删去边以及依赖删去边。
以上图为例,我们从 开始向上找到的环边的两端分别是 ,我们从 开始进行树上动态规划。
- 依赖非删去边:
删去边 之后,节点 不能够依赖于 ,结果是选取 的情况中,必有 中的一个不被选取。而这个时候 节点是否被选取都不重要,统计答案 。
- 依赖删去边:
现在 的选取一定依赖于 的不选取,答案就是 ,而这个时候 的子节点可以任选。
删去边的方式
仍然以上图为例:只要一条边指向的 节点不是起点 ,说明这条边就不是删去边,就可以正常处理。
代码
一个小的细节是,vector<bool> 有着极大的优化,几乎等同于 bitset,非常好用。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
| #include<bits/stdc++.h>
inline int read() {
int x = 0;
char ch = getchar();
while (!isdigit(ch))
ch = getchar();
while (isdigit(ch))
x = x * 10 + ch - '0', ch = getchar();
return x;
}
using namespace std;
const int INF = 0x3f3f3f3f;
const int MAXN = 1000005;
int n, ans;
int lt, rt;
int edgeCount;
int head[MAXN], toNode[MAXN], nextEdge[MAXN];
vector<bool> vis;
int control[MAXN];
int fTree[MAXN][2];
inline void addEdge(int from, int to) {
edgeCount++;
toNode[edgeCount] = to;
nextEdge[edgeCount] = head[from];
head[from] = edgeCount;
return;
}
int dpTree(int from, bool isDelete) {
fTree[from][0] = fTree[from][1] = 0;
vis[from] = true;
int gap = INF;
for (int i = head[from]; i; i = nextEdge[i]) {
int to = toNode[i];
if (to ^ lt) {
vis[to] = true;
int res = dpTree(to, isDelete);
fTree[from][0] += res;
gap = min(gap, res - fTree[to][0]);
}
}
fTree[from][1] = fTree[from][0] + 1 - gap;
if (!isDelete && from == rt)
fTree[from][1] += gap;
return max(fTree[from][0], fTree[from][1]);
}
int main() {
n = read();
vis.resize(n + 1, false);
for (int i = 1; i <= n; ++i)
addEdge(control[i] = read(), i);
for (int i = 1; i <= n; ++i)
if (!vis[i]) {
for (lt = i; !vis[control[lt]]; vis[lt] = true)
lt = control[lt];
rt = control[lt];
int max1 = dpTree(lt, true);
dpTree(lt, false);
int max2 = fTree[lt][0];
ans += max(max1, max2);
}
cout << ans;
return 0;
}
|
闲话
本人在校测中使用的方法就是分成环和树,结果打了 行代码,刚好多了 行,并且直到比赛结束都没能调试成功。使用了骗分大法,输出每棵基环树结点个数的一半,竟然得了 分。