来源：2025/07/31 SDOI_2025

P2014 [CTSC1997] 选课
P1273 有线电视网
P2018 消息传递
P2569 [SCOI2010] 股票交易

题单题解 Dynamic Programming

“动态规划并非一种编程技巧，而是一种思考复杂多阶段决策问题的数学方法。它利用最优子结构的性质，将大问题分解为一系列相互关联的子问题，通过递归式的贝尔曼方程实现整体最优。” —— 理查德·贝尔曼

树形 DP

显然的，依赖关系呈现树形结构，而这类的通用思路就是依据子树进行阶段划分。

由于树形结构，dfs 就是我们代码实现的方式，而状态转移就在回溯阶段。我们合并统计子树带来的结果，推出当前节点为根的子树的最优子结构，然后再传回上一级，最终传给整棵树的根。这时，f[root] 就累积了对整棵树的统计。

所以框架是一定的，这导致状态定义的一维就是限定在以 i 为根的子树内。最重要的还是状态的描述以及转移过程。由于树形结构的特殊依赖关系，状态的转移也可以会相对复杂。

P2014 [CTSC1997] 选课

建立源点，把森林无代价无收益地连起来，构成一棵树；
题意理解，发现课程 u 是代价为 1，收益为 s[u] 的物品，背包容量是 m；
给出定义，f[u][cost] 代表以 u 为根的子树内代价为 cost 的最大收益；
处理边界，f[u][1] 显然的就是只选择自己，为 s[u]；
考虑转移，f[u][cost] = max(f[u][cost], f[u][cost - j] + f[v][j]；
修订细节：
- 对于 u，其更新顺序应该是 cost 从大到小，原理与 01 背包相同；
- 对于 v，考虑 j < cost，因为 u 必选，占用了一个名额；

这道题目就做完了，整个流程格式化，而且就是背包的模版。唯一的转移限制也很显然，是一个比较合适的【模版】树上背包。

#include<bits/stdc++.h>

using namespace std;

const int MAXN = 305;
const int MAXM = 305;

int n, m;

int edgeCount;
int head[MAXN], toNode[MAXN], nextEdge[MAXN];

int siz[MAXN];
int f[MAXN][MAXM];

inline int read();

inline void addEdge(int from, int to) {
    edgeCount++;
    toNode[edgeCount] = to;
    nextEdge[edgeCount] = head[from];
    head[from] = edgeCount;
    return;
}

inline void dp(int from) {
    siz[from]++;
    for (int i = head[from]; i; i = nextEdge[i]) {
        int to = toNode[i];
        dp(to);
        siz[from] += siz[to];
        for (int j = m; j >= 0; --j) {
            int assign = (from == 0 ? j : j - 1);
            assign = min(assign, siz[to]);
            for (int k = 0; k <= assign; ++k)
                f[from][j] = max(f[from][j], f[from][j - k] + f[to][k]);
        }
    }
}

int main() {
    n = read(), m = read();
    for (int i = 1; i <= n; ++i) {
        addEdge(read(), i);
        f[i][1] = read();
    }
    dp(0);
    cout << f[0][m];
    return 0;
}

P1273 有线电视网

这个题输入相对复杂一点，细心处理即可。

主要是对于问题的转化：

使得有线电视网在不亏本的情况下使观看转播的用户尽可能多。

这句话给的范围很宽，“不亏本的情况下”。我们考虑两个可能的情况 S1, S2 ，他们都做到了“尽可能多”的用户，但是 profit(S2) > profit(S1)，这时选择 S2 一定不会更劣。

换句话说，对于一个给定的观看人数 man，如果存在一个解使得电视网不亏本，那么最大利润一定不亏本。

所以我们就去找最大利润即可。

以上内容对于所有的动态规划题目都是一样的，难度也都在这里，想清楚了就容易了。以下是格式化的流程：

f[u][man] 表示在以 u 为根的子树内让 man 个人观看的最大利润；（如果是亏损就是最小亏损，反正是金钱数量最大值）
f[u][man] = max(f[u][man], f[u][man - k] + f[v][k] + weight);，这个转移显然是正确的，也是容易想到的，但是有一个时间复杂度的问题：枚举 v 是的，枚举 k 也是，总体上是的，然而事实上是跑得飞快。

这种做法的人还不赶快给出数据的人磕一个！Oπ

其他的没什么，下面是这种方法的代码：

#include<bits/stdc++.h>

using namespace std;

const int MAXN = 3005;
const int INF = 0x3f3f3f3f;

int n, m;

int edgeCount;
int head[MAXN], toNode[MAXN], nextEdge[MAXN];
int weight[MAXN];

int siz[MAXN];
int money[MAXN];
int f[MAXN][MAXN];

inline void addEdge(int from, int to, int w) {
    edgeCount++;
    toNode[edgeCount] = to;
    weight[edgeCount] = w;
    nextEdge[edgeCount] = head[from];
    head[from] = edgeCount;
    return;
}

inline void dfs(int from) {
    if (from > n - m) {
        siz[from]++;
        f[from][1] = money[from];
        return;
    }
    for (int i = head[from]; i; i = nextEdge[i]) {
        int to = toNode[i];
        dfs(to);
        siz[from] += siz[to];
        for (int j = siz[from]; j; --j)
            for (int k = 0; k <= siz[to]; ++k)
                f[from][j] = max(f[from][j], f[to][k] + f[from][j - k] - weight[i]);
    }
    return;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    cin >> n >> m;
    for (int i = 1; i <= (n - m); ++i) {
        int siz, to, w;
        cin >> siz;
        while (siz--) {
            cin >> to >> w;
            addEdge(i, to, w);
        }
    }
    for (int i = (n - m + 1); i <= n; ++i)
        cin >> money[i];

    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= m; ++j)
            f[i][j] = -INF;

    dfs(1);
    
    for (int i = m; i >= 0; --i)
        if (f[1][i] >= 0)
            cout << i, exit(0);
    return 0;
}

那么显然的，饱受复杂度之扰和卡常出题人之苦的我们一定要找到一个时间复杂度正确的算法！（没错，这个问题在选课的超小数据量下被隐藏了，真是可恶。）

思路就是后序遍历。这里蒟蒻不觉得可以写得比这篇题解更好，所以就贴个链接，大家仔细阅读品鉴，并且重构自己的代码。

这个方法好就好在他把树形结构打散了，用一种特殊的顺序，把以子树为单位合并这件事情转化到了序列上，同时是 dfs 序的通病：子树下标在一段区间内，所以还可以进行子树和非子树的 siz 跳转。（剖剖爱好者看后爽极）

所以可以考虑重构一下以上两道题的代码，不过 T1 蒟蒻懒得重新整了，下面贴出 T2 的代码：

不过可笑的是，应该是由于随机小数据，每次理论最差操作还远远跑不满，这个复杂度正确的做法和原做法用时几乎一模一样。

但是肯定有用到的时候……后序遍历法万岁！

#include<bits/stdc++.h>

using namespace std;

const int MAXN = 3005;
const int INF = 0x3f3f3f3f;

int n, m;
int mon[MAXN];

int edgeCount;
int head[MAXN], toNode[MAXN], nextEdge[MAXN];

int countDfn;
int siz[MAXN], ind[MAXN];
int f[MAXN][MAXN];

inline int read();
inline void addEdge(int from, int to) {
    edgeCount++;
    toNode[edgeCount] = to;
    nextEdge[edgeCount] = head[from];
    head[from] = edgeCount;
    return;
}

inline void init() {
    n = read(), m = read();
    for (int i = 1; i <= (n - m); ++i) {
        int cnt = read();
        while (cnt--) {
            int to = read();
            mon[to] = -read();	// 这里考虑边权下放点权
            addEdge(i, to);
        }
    }
    for (int i = (n - m + 1); i <= n; ++i)
        mon[i] += read();		// 与刚刚下放的点权对冲
    return;
}

inline void dfs(int from) {
    siz[from]++;
    for (int i = head[from]; i; i = nextEdge[i]) {
        int to = toNode[i];
        dfs(to);
        siz[from] += siz[to];
    }
    countDfn++;
    ind[countDfn] = from;
    return;
}

int main() {
    init();

    dfs(1);

    for (int i = 0; i <= countDfn; ++i)
        for (int j = 1; j <= m; ++j)
            f[i][j] = -INF;
    // 注意初始化 i = 0 也要赋值，因为被依赖了
    for (int i = 1; i <= countDfn; ++i) {
        int from = ind[i];
        for (int j = 1; j <= m; ++j) {
            if (from >= (n - m + 1))
                f[i][j] = max(f[i - 1][j - 1] + mon[from], f[i - siz[from]][j]);
            else
                f[i][j] = max(f[i - 1][j] + mon[from], f[i - siz[from]][j]);
        }
    }
    
    for (int i = m; i >= 0; --i)
        if (f[countDfn][i] >= 0)
            cout << i, exit(0);
    return 0;
}

P2018 消息传递

这个题目比较奇怪，“每次传递一个”导致了其特殊性，这和普通的 Bfs 和树的重心就完全不同了。

首先一些比较显然错误的贪心策略：最大的子树、度数最大的子树、等等。如果度数大，已经传递了的节点就可以在较长时间内持续做出贡献；如果子树大，那么大的在运行的同时还可以运行小的。所以单一的考虑是有问题的。

回归到动态规划上来，我们要的是最优子结构，能够决定顺序的，一定是他们的结果，因为这代表了整个状态的贡献，而不是状态中的某一个特征。

所以考虑计算出各个子树所用时间之后，按照所需时间从大到小进行传递，比较的贪心，但是贪得东西是有动态规划性的。

格式化过程就不展示了，因为相似性过高，自己思考之后看代码也会很容易。

下面是代码：

#include<bits/stdc++.h>

using namespace std;

const int MAXN = 1005;

int n;

int edgeCount;
int head[MAXN], toNode[MAXN << 1], nextEdge[MAXN << 1];

int f[MAXN];

vector<int> son;

int t = 0x3f3f3f3f;
vector<int> ans;

inline void addEdge(int from, int to) {
    edgeCount++;
    toNode[edgeCount] = to;
    nextEdge[edgeCount] = head[from];
    head[from] = edgeCount;
    return;
}

inline void dfs(int from, int father) {
    for (int i = head[from]; i; i = nextEdge[i]) {
        int to = toNode[i];
        if (to != father)
            dfs(to, from);
    }
    
    for (int i = head[from]; i; i = nextEdge[i]) {
        int to = toNode[i];
        if (to != father)
            son.push_back(to);
    }
    if (son.empty())
        return f[from] = 1, void();
    
    sort(son.begin(), son.end(), [](int a, int b) {
        return f[a] > f[b];
    });
    for (size_t i = 0; i < son.size(); ++i)
        f[from] = max(f[from], f[son[i]] + (int)i + 1);
    son.clear();
    return;
}

inline void solve() {
    for (int i = 1; i <= n; ++i) {
        son.clear();
        memset(f, 0, sizeof(f));
        dfs(i, 0);

        if (t > f[i]) {
            ans.clear();
            t = f[i];
            ans.push_back(i);
        } else if (t == f[i])
            ans.push_back(i);
    }
    return;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    cin >> n;
    for (int i = 2; i <= n; ++i) {
        int fat;
        cin >> fat;
        addEdge(fat, i);
        addEdge(i, fat);
    }
    solve();
    cout << t << '\n';
    for (int i : ans)
        cout << i << ' ';
    return 0;
}

单调队列优化 DP

P2569 股票交易

读题

这个题目比较麻烦，因为涉及的参数比较多，我们慢慢看。

是收益最大化问题，这个应该就是我们 f[][] 所保存的东西；
有一条时间线，这个划分了阶段，因为每一天都有属于自己的参数，我们最终的询问也是第 T 天的值；
有很多的限制，手上最多持有的股票、一次交易（一天之内）能交易的最大的量，这个限制了我们转移的路径，在代码中的体现可能就是循环的边界以及各种 continue;

状态定义

这个是很显然的，f[i][j] 表示经过前 i 天，且在第 i 天手上持有 j 个股票的最大利润，而我们求的就是 f[T][j] 中的最大值。

暴力转移

这一部分时首先要理解清晰的，包括题目中的含义，类似的用法以及在 f 表中数据的指向方式。

我们状态之间分成“变”和“不变”两种传递方式：

不变，这意味着我们的初始状态或者是上一次“变”带来的影响可以延续到后续的某一天；
变，这个可能是买入股票使持有量增加，或者是卖出股票使持有量减少。从这里可以看出，我们并不能只看持有量就能分析过程，而是要分析买入和卖出，其转移的终点不过是通过初始状态和以上两种操作计算出来的位置罢了。

所以 f[day][now] 可能的更新来源就有以下几个：

f[day - 1][now]，不变，和昨天一样；
f[day - 1][k], k < now，变了，买入了一些（now - k）股票；
f[day - 1][k], k > now，变了，卖出了一些股票；

那有些同学就要问了：

欸？之前的不是可以一直延续吗？你为什么只考虑了昨天（day - 1）？

回想一下我们简化的完全背包的代码，它和 01 背包的区别在于费用维的遍历顺序。它是从小到大的：

1
2
3

for (int i = 1; i <= n; ++i)
    for (int j = cost[i]; j <= m; ++j)
        f[j] = max(f[j], f[j - cost[i]] + val[i]);

这个导致了我们可以使用刚刚更新过的值再次加上 val[i] 继续得到新的值，隐式地让 i 物品被选取了多次。

这里的道理也是一样，我们说有一种操作叫做“不变”，我们对于传递过来的东西不变，但是传递过来的东西也可以是前一个阶段不变过来的，所以我们可以只关注昨天 day - 1。我们对于每个 day 中 now 只股票的情况，都看一遍 day - 1，看看从哪天怎么转过来是最好的即可（也就是找结果的最大值）。

这个时候我们经过了很多思考，十分满足，觉得和正解近在咫尺，不过是和嘛 QAQ。

优化转移

这部分我们用表格图进行演示，并且讲清楚单调队列的使用方式。

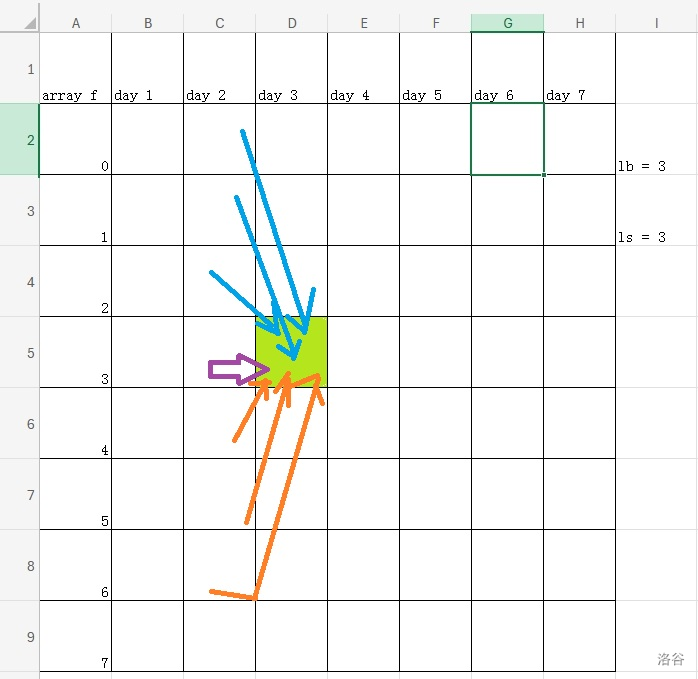
窗口操作

如上图所示，假如我们考虑第三天手上留有三只股票的情形。

紫色箭头就是“不变”的策略，我们直接继承第二天手上就有的 3 只股票也行；
注意到右边的小字，我们一天之内只能买卖最多 3 只股票，这意味着蓝色箭头是可行的，他们买的股票数量都不超过三只；同时橘色箭头也是可行的，因为卖了不超过 3 只。但是我们不能从 day 2, 7 的情况转移过来，因为它需要卖掉 4 只股票才能达成我们期望的状态，而这是不可行的，这就是所谓路径被限制了。

这是两个对于 day 1, day 2 但是不同只股票的情况，先只考虑买入。

绿色的点是末状态，橘色的点是可以转移到绿色点的状态，容易发现这是一个窗口，长度为三（当然可以小于三，比如只有一只股票的时候）。这意味着整个在更新的过程中，我们不必要把 day - 1 重看一遍，我们作为近视眼，在 now + 1 能够多看到的，就是 day - 1 的 now 位置，而丢掉的就是 now - lb 位置。

这个对于卖出是一个一模一样的过程，唯一的差别在于顺序，因为卖出的窗口向下长的，所以从下向上考虑，不再赘述。

我们每讨论完一个 now，就对应的丢掉 day - 1 的窗口末端，把 day - 1, now 加入考虑。如果，我们有一种数据结构，在完成这次更新之后还能立刻告诉我窗口内部转移结果最大值，这样子扫描过程就变成的了！

单调队列

在经典的【模版】题目“滑动窗口”中，我们就是需要维护一个这样的数据结构。

在这里，我们希望找到限制以内的最优解，而且当当前最优解掉到外面去的时候，我们还知道谁顶上来。俗话说的好：

如果一个选手年纪比你小而且考得比你好，你就没有希望了。

这句话的意思就是，他会在你的近视窗口范围内更久，给更多的未处理的点带来贡献，而且贡献还比你大，你就不会被考虑了。相信大家现在都理解为什么可以舍弃掉一部分了。

所以单调队列就是这样的，它是一个队列，内部具有单调性。一个后加入的值 cur 如果比先加入的值 pre 要大，那 pre 就可以滚出去了，我们不需要它，它没有用处，cur 可以完美地代替它的位置，而且做得比它还好。

我们一直这样让吊车尾滚出去，直到 cur 遇上了一个比它厉害的大牛 orz，在目前，我们的数据还是由 orz 以及 orz 前面的神犇更新的，但是当大牛和神犇退去的时候，就到了 cur 顶上来的时候了。

这就是我对单调队列的简单介绍，如果觉得有趣但是没有用，那就去看那个模版题的题解吧。

我们要维护什么？

注意到状态转移方程：

f[day][now] = max(f[pre][k] - pb[day] * (now - k));，这是买入；
f[day][now] = max(f[pre][k] + ps[day] * (k - now));，这是卖出；

学过分数线的同学都知道，分离常数或者参变分离是很有用的，我们维护数据也是如此。对于一个给定的 day, now, pre，可以认为只有 k 一个变量。所以我们把含有 k 的部分提出来：

f[pre][k] + pb[day] * k，这是买入；
f[pre][k] + ps[day] * k，这是卖出；

我们只需要搞一个单调队列，把这些值和下标丢进去，然后按照标准程序走就行了：

检查是否为空和队头是否合法（在考虑范围内）；
用队头更新当前值；
让实力不足的吊车尾滚出去；
把当前新考虑得值加到里面去；

代码

#include<bits/stdc++.h>

using namespace std;

const int MAXN = 2005;
const int INF = 0x3f3f3f3f;

int T, MaxP, W;

int pb[MAXN], ps[MAXN];
int lb[MAXN], ls[MAXN];

deque<int> val, ind;
int f[MAXN][MAXN];

inline void init() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    cin >> T >> MaxP >> W;
    for (int i = 1; i <= T; ++i)
        cin >> pb[i] >> ps[i] >> lb[i] >> ls[i];
    return;
}

int main() {
    init();

    for (int i = 0; i <= T; ++i)
        for (int j = 0; j <= MaxP; ++j)
            f[i][j] = -INF;
    f[0][0] = 0;
    for (int day = 1; day <= T; ++day) {
        int pre = max(0, day - W - 1);

        /*--- transform through buy ---*/
        val.clear();
        ind.clear();

        for (int now = 0; now <= MaxP; ++now) {
            f[day][now] = max(f[day][now], f[day - 1][now]);

            while (!ind.empty() && ind.front() <= now - lb[day] - 1) {
                ind.pop_front();
                val.pop_front();
            }


            if (!ind.empty())
                f[day][now] = max(f[day][now], val.front() - pb[day] * now);

            int curVal = f[pre][now] + pb[day] * now;
            while (!ind.empty() && val.back() <= curVal) {
                ind.pop_back();
                val.pop_back();
            }
            val.push_back(curVal);
            ind.push_back(now);
        }

        /*--- transform through sell ---*/
        if (pre != 0) {
            val.clear();
            ind.clear();

            for (int now = MaxP; now >= 0; --now) {
                f[day][now] = max(f[day][now], f[day - 1][now]);

                while (!ind.empty() && ind.front() >= now + ls[day] + 1) {
                    ind.pop_front();
                    val.pop_front();
                }

                if (!ind.empty())
                    f[day][now] = max(f[day][now], val.front() - ps[day] * now);

                int curVal = f[pre][now] + ps[day] * now;
                while (!ind.empty() && val.back() <= curVal) {
                    ind.pop_back();
                    val.pop_back();
                }
                val.push_back(curVal);
                ind.push_back(now);
            }
        }
    }
    
    int ans = 0;
    for (int i = 0; i <= MaxP; ++i)
        ans = max(ans, f[T][i]);
    cout << ans;
    return 0;
}

Do not go gentle into that good night.

题单：动态规划 01