学术：详解 Treap & FHQ

前言

BST 和 Heap 都是两个可以有很多等效结构的数据结构，这种灵活性让他们具有了同时维护的可能性。而 Treap 就是这样一种结合的产物。

Treap 有一个很方便的点：他完全分化了职责，数据处理交给 BST，平衡性交给 Heap，所以只要在平衡树旋转或者依据路径拆合的过程中，注意一下 key 值带来的顺序即可。所以这些操作不管有多么花哨，只要保证了堆性质，就可以保证一定的平衡性，而不用担心退化问题。

本文涉及的 zig, zag, split, merge 操作都是 Cpp 语言之美的体现，传参传地址和灵活的递归让代码实现非常简洁，同时让初学者脑壳痛，难以理清楚具体的运行过程，下面进行解析。

Treap 的旋转

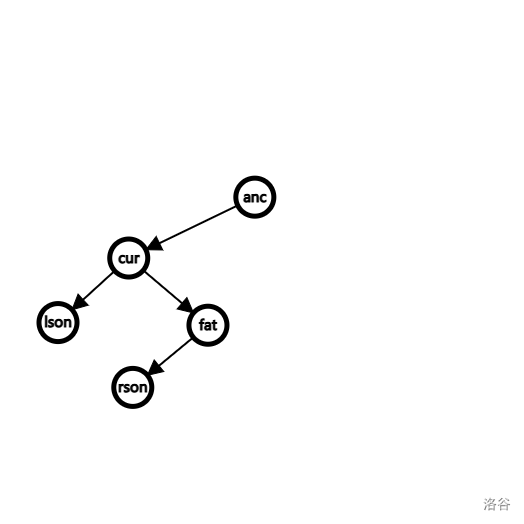
我们说对节点 fat 进行右旋，指的是把 fat 向右下方按到下面去，而把他的儿子 cur 提起来，放在自己的位置，下面是代码以及图解过程。

关于左旋……右旋都会了，左旋就对代码异或一下，原理也是一样，不多废话。

代码

请注意这份代码其实并不简洁，很多地方为了方便理解而特殊设置，比如临时变量 fat 和 ancSon 这么奇怪的变量名，所以请理解之后根据自己的习惯打磨属于自己的板子。

inline void zig(int& ancSon) {
  int fat = ancSon;
  int cur = lson(fat);
    lson(fat) = rson(cur);
    rson(cur) = fat;
    pushUp(fat);
    pushUp(cur);
    ancSon = cur;
    return;
}

图解

这是原来的树的形态（其他子树，不涉及改动，也不好看，就没有显示）：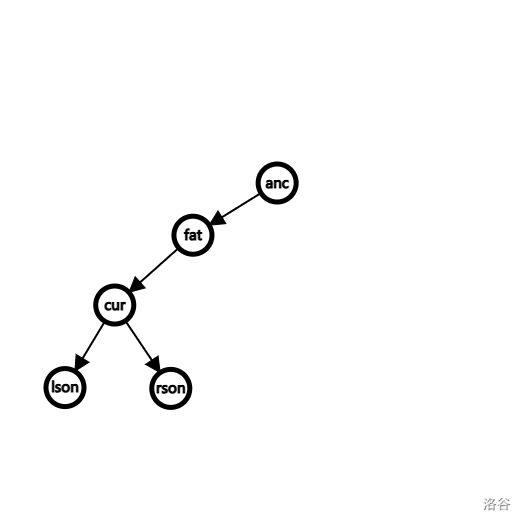

lson(fat) = rson(cur)，安排 rson 的后事，让 fat 来接管，满足 BST 性质，且让父子关系改变（把这种中间状态映射到父子之类的人人关系上还是太抽象了）。

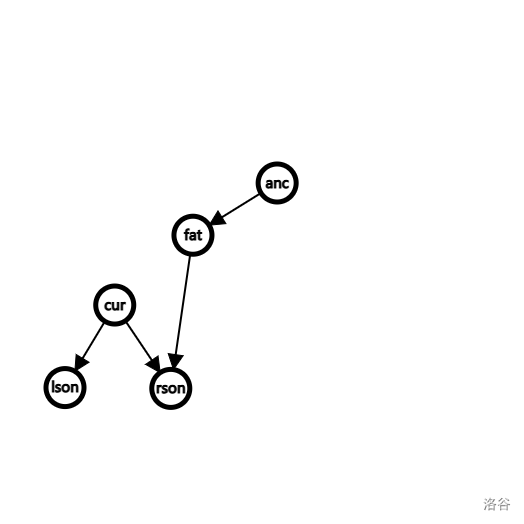
rson(cur) = fat，注意 rson 后改动，不然原本的 rson 就没人接管，被丢掉了。这个时候已经看到 fat, cur 已经构建成了反的父子关系。

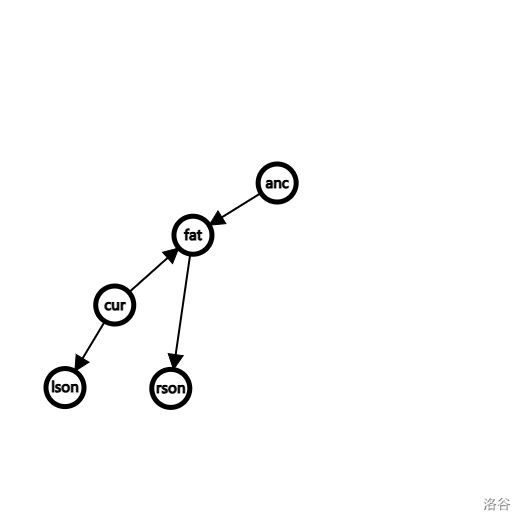
不过与 fat 产生关系的还有 fat(fat)，也就是 anc。

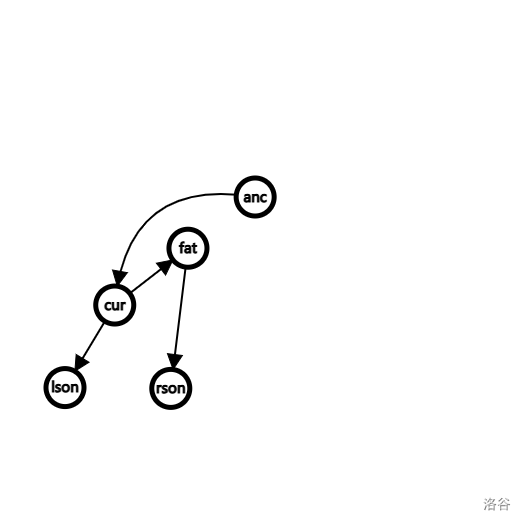
这一点是比较不好从代码层面上理解的，所以这里我把传参的名字改成了 ancSon。虽然逻辑上和 fat 是一个东西，但是在存储上完全不同。ancSon = cur 的意思就是让来自 anc 的指针指向 cur，所以在后文 FHQ 的 split 操作时，我愿意把它命名为 link。不过熟悉之后就没有写成这样的必要了。

处理了这个，逻辑上就完善了，整理一下可视化就是最后的样子。

FHQ 的 Split & Merge

Split

inline void split(int p, int v, int& linkA, int& linkB) {
    if (p == 0)
        return linkA = linkB = 0, void();
    if (val(p) <= v) {
        linkA = p;
        split(rsn(p), v, rsn(p), linkB);
    } else {
        linkB = p;
        split(lsn(p), v, linkA, lsn(p));
    }
    pushUp(p);
    return;
}

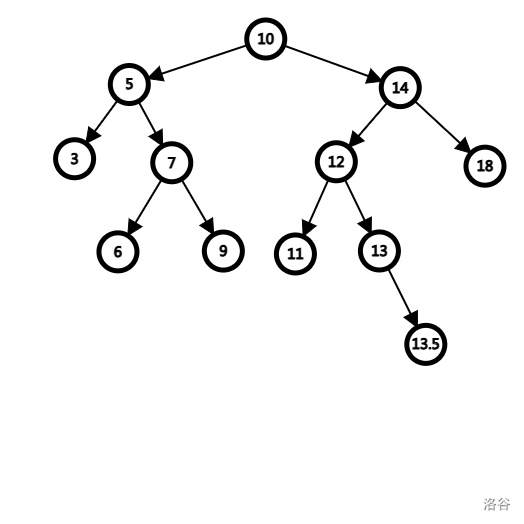
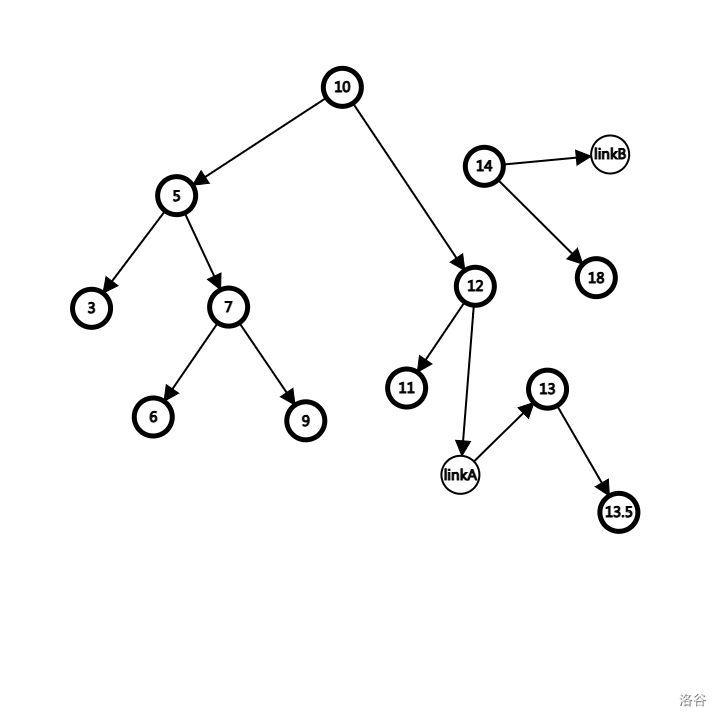
先说 Split，祭上这个上课时 why 的手绘图，而我们照样去 split(13)。

接下来是视觉盛宴，请欣赏（不要在意作图的时候一些小细节）。

我们首先创建 linkA, linkB，这个时候都还是初始的，也就是 split 函数当中创建的变量。

我们发现 10 < 13，于是让 linkA 为 10 节点。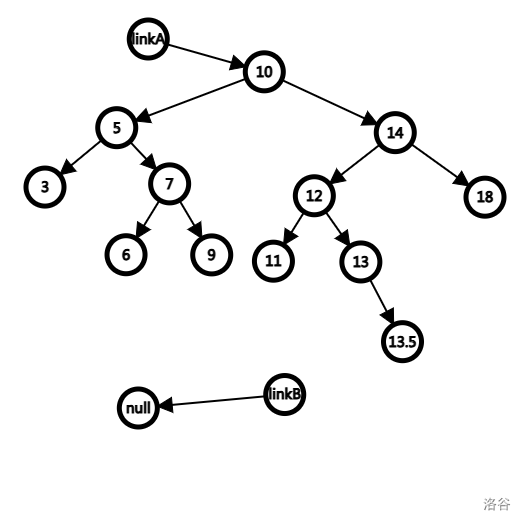

接下来递归调用下一层，此时传入的函数参数 linkA 实际上是 10 节点的右儿子，这意味着下图的关系：10 的右儿子处于待定状态，而不再是原来的 14 节点。这个时候，我们可以保证 10 以及其左子树一定是小于 13 的，但是其右子树仍然有小于 13 节点存在的可能性，所以继续向右寻找。

split(rson(p), v, rson(p), linkB)

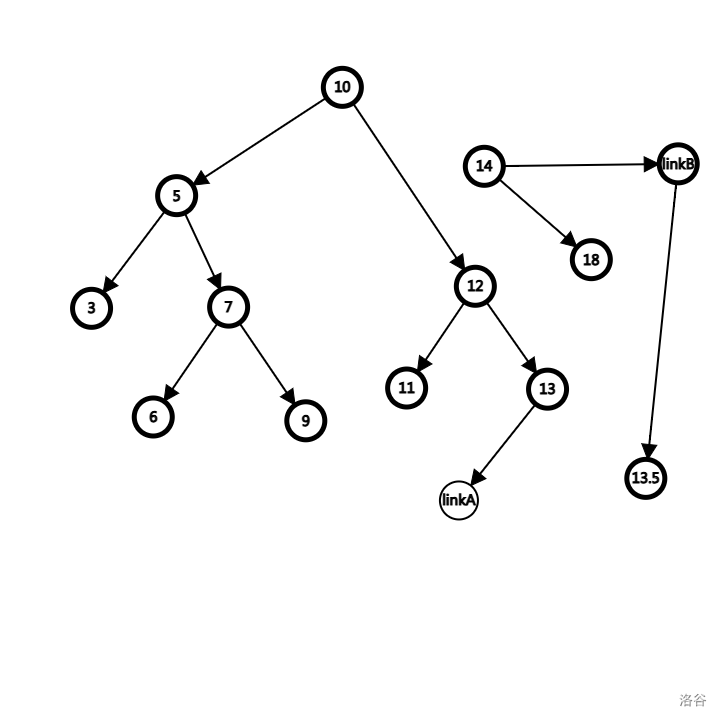
请注意，后续操作中有赋值语句更改 rson(p)，所以逻辑上 10, 14 处于断开状态，但是存储上，调用的时候的第一位 rson(p) 仍然是 14 节点。

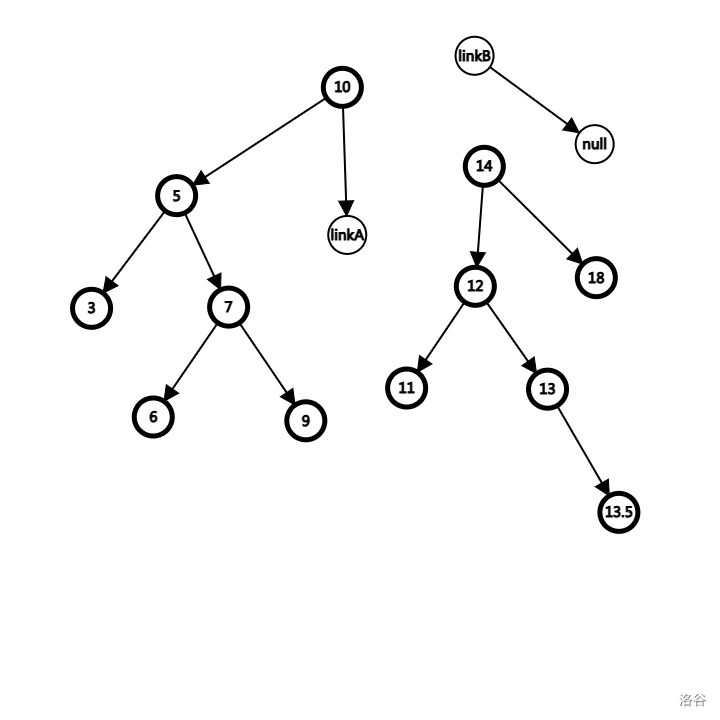
同理，当我们向右继续寻找的时候，发现 14 > 13，于是让 linkB 指向 14 节点，然后向不确定的左子树继续寻找。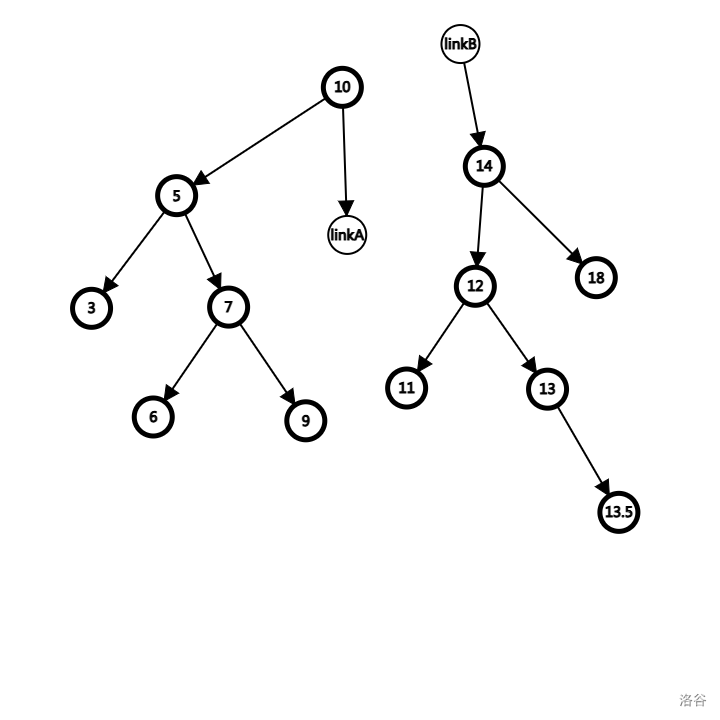

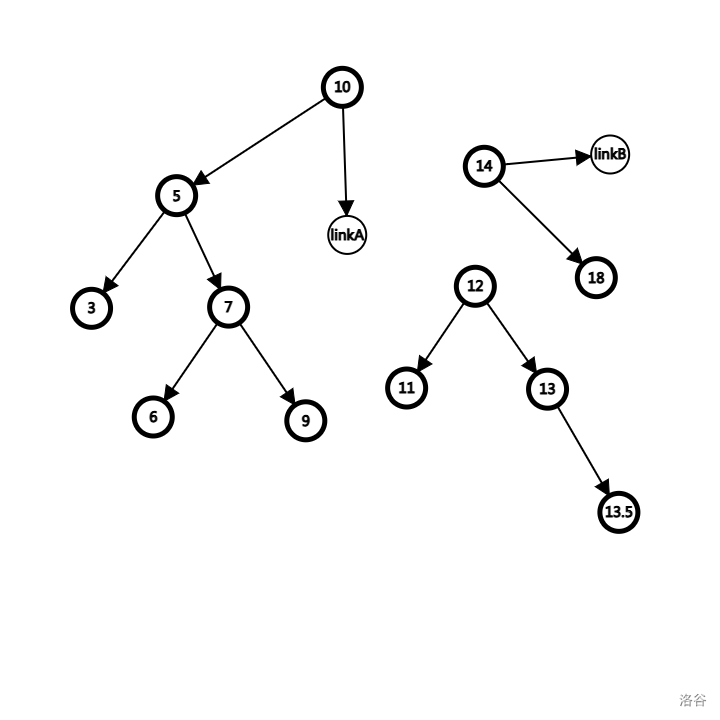
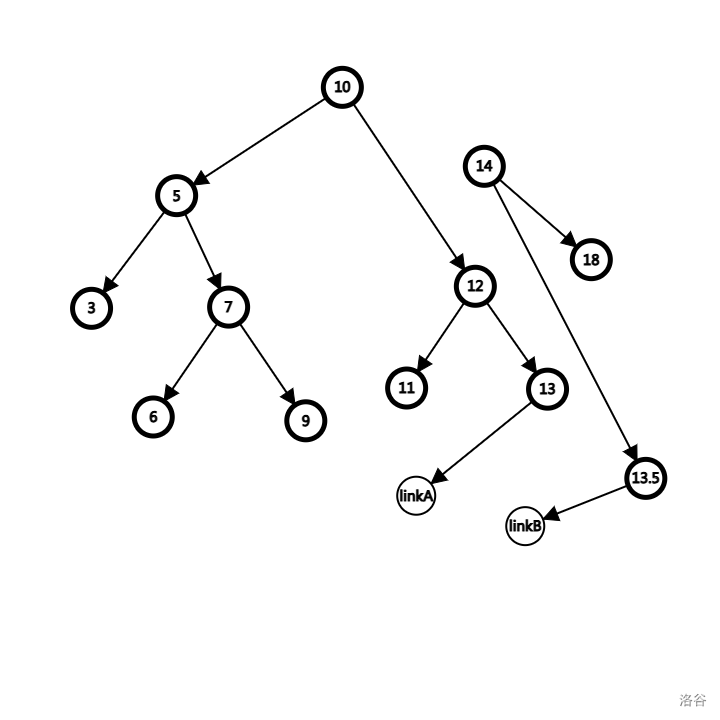
发现 12 < 13，这意味着我们的传参 linkA，其本质是 rson(10 节点)，要进行赋值语句了。

linkA = p;

这就是下面这一步 linkA 指向 12 节点所体现的。其余的操作一致，自行理解，不再赘述。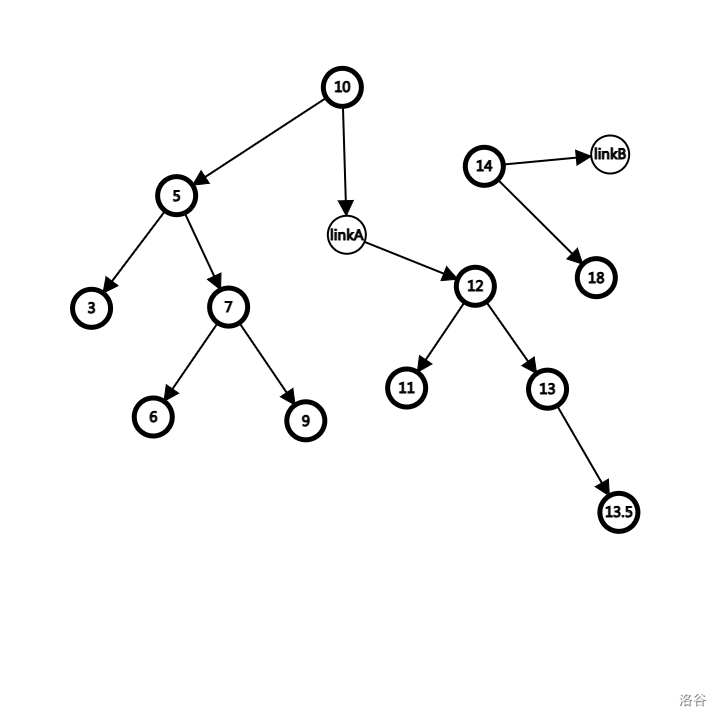

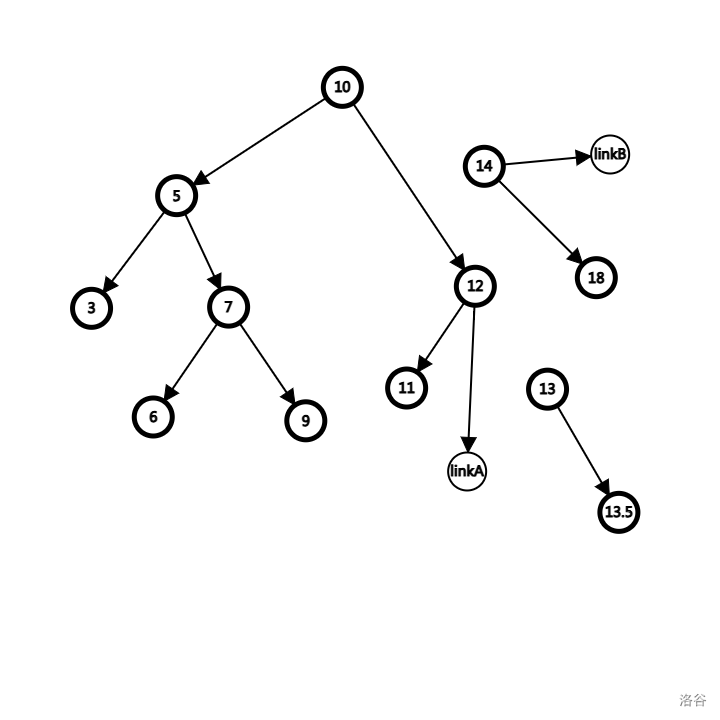
在这里我们继续向 13.5 的左子树走下去，发现 p == 0，意味着两棵树已经被完全分开了。我们每次借助 linkA, linkB 的传承，每一步都拆掉了一条边。在走完 10 -> 14 -> 12 -> 13 -> 13.5 的一条根到叶子的路径之后，我们就成功用 O(logN) 的时间复杂度把整棵树劈开了。此时，linkA, linkB 就指向原来留存的空节点 0 即可。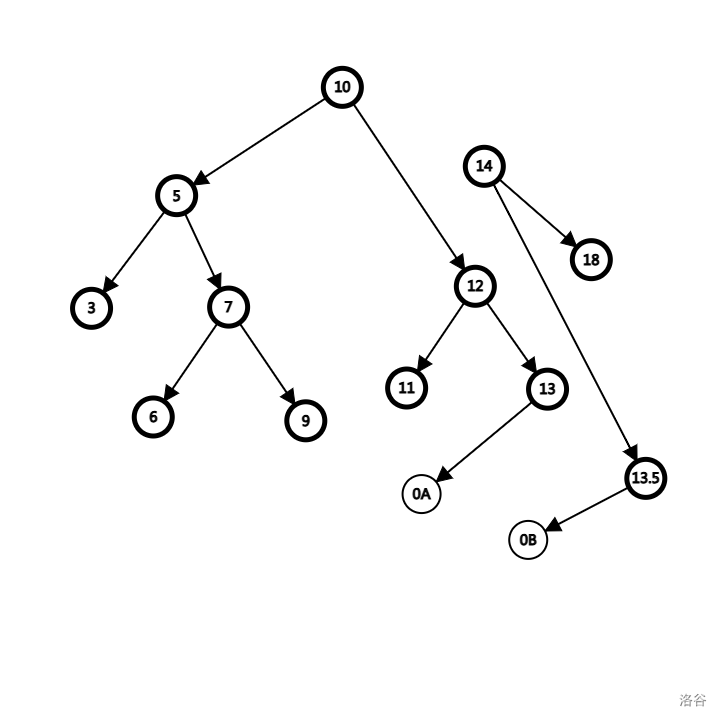

可视化整理一下就是这个样子，很好看。根据上文，沿着一条路径剖开，其相对位置是保持不变的，所以 Tree 性质和 Heap 性质都没有被破坏掉，是非常完美的一个处理平衡树的思路。（小蒟蒻本以为旋转就是灵活性的极限了，没想到还有狠人）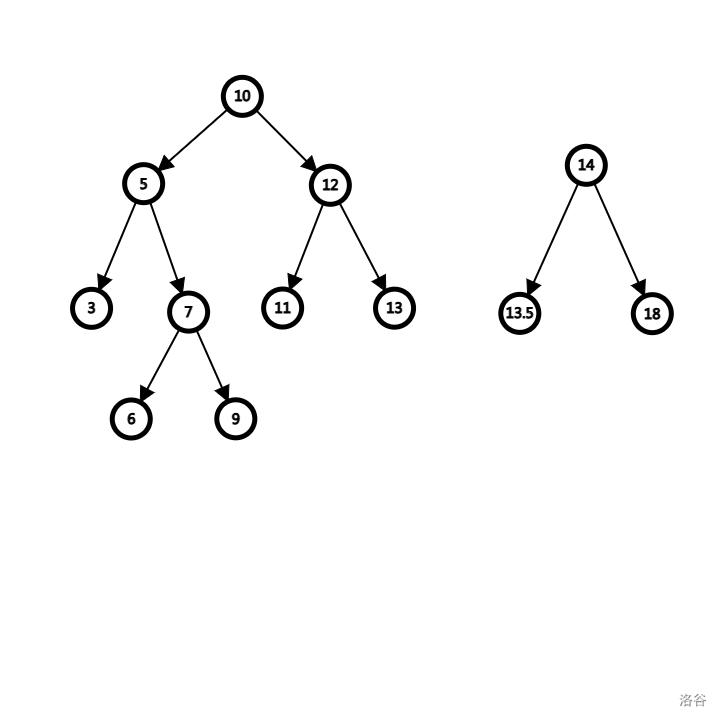

Merge

关于 Merge，其实也就好理解了。这其实就是一个争儿子的过程。

inline int merge(int linkA, int linkB) {
    if (!linkA || !linkB)
        return linkA + linkB;

    if (key(linkA) > key(linkB)) {
        rsn(linkA) = merge(rsn(linkA), linkB);
        pushUp(linkA);
        return linkA;
    } else {
        lsn(linkB) = merge(linkA, lsn(linkB));
        pushUp(linkB);
        return linkB;
    }
}

这里假设 val(A) < val(B), key(A) > key(B)。

考虑对 rtA, rtB 进行合并。首先根据 key 值，rtA 肯定是父亲。那么问题就是合并之后 rtA 有两个可能的右儿子：rson, rtB，因为都满足 Tree 性质和 Heap 性质。所以怎么办呢，要考虑对 rson, rtB 进行合并。

容易发现是递归处理的，因为在缝合路径上都会存在多了一个儿子的问题，直到到达叶子节点，那个时候就是我们的决策边界。我们只需要 return 一下到底谁才是最后的根，随后其他节点依次根据下方传来的判断更新即可。容易发现还是一个根到叶子的路径，仍然是 O(logn) 的复杂度。

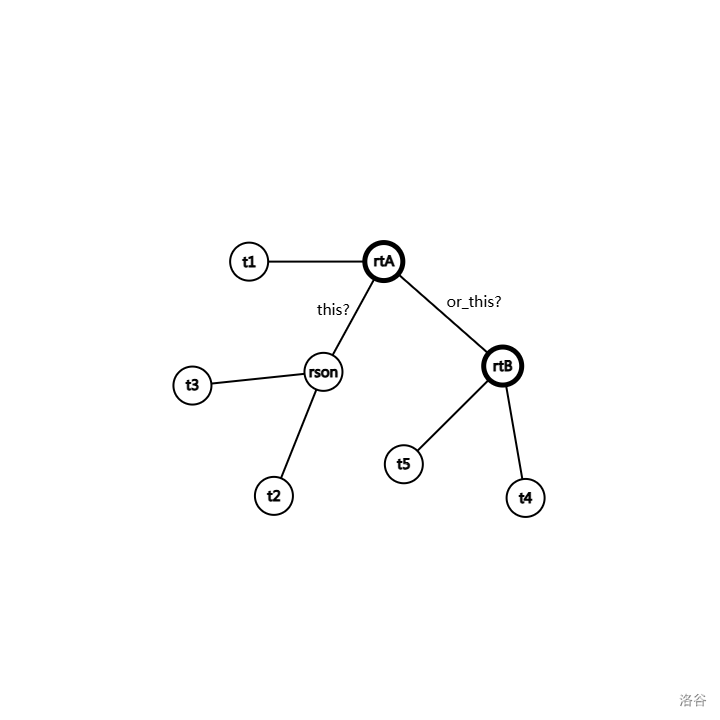
希望读完以后能够让大家有更深刻的理解。以上，感谢。

update：

由于 graph editor 的灵活性，在 linkA 接到 13 节点下方是，应该是右儿子。（它自己飘到左边去了）